Today we’re going to be looking at figuring out how to calculate the execution of polyrhythms. It can seem difficult trying to figure out how to divide a beat into different numbers evenly, especially if they’re odd or prime numbers. But all it is is simple math, and once you have the system down, it’s pretty automatic and you can even find patterns that are even more helpful (and you probably learned those in music school if you went).
Before we start with that, I also want to introduce a new subsection of the website: labs.seanchenpiano.com. I have a lot of programming projects that I’ve worked on throughout the years, and I’m going to try to finish them up and put them on. They won’t be super polished at first, and will receive many updates after publication. Right now, there’s only one thing on there, and that is a polyrhythm metronome app. It should work on most browsers and devices, but let me know in the comments if anything is buggy, or any feature requests!
Preface
Polyrhythms are usually not meant to be performed exactly mathematically correct. Oftentimes it is just a composer trying to fit more notes into a beat, or maybe the composer wants the de-synchronization as part of an affect or expression, and not necessarily the precise division. But just like with many expressive techniques, I think it is important to know what the baseline is — what it should precisely be — before you add in rubato or other personal touches. So, just to be clear, I’m not advocating for metronomic or robotic execution of polyrhythms.
Definition
So what are polyrhythms? It happens when you have two or more voices going, and each of them are dividing a beat into different tuples. Tuples are just a subdivision of beats: duples, triplets, quadruplets, etc. The most common of polyrhythms is 3 against 2 or 2 against 3, written 3:2 or 2:3, and most musicians learn how to execute those early on. I’m not aware of any tradition or logic behind what number goes where; for me, as a pianist, it seems that the first number corresponds to the right hand and the second to the left hand, though I can see it being interpreted as the second number being the general beat of the passage, and the first number being the “ornament” or deviation.

The Problem
We want to find a method so that we can be 100% sure of where the micro-beats should lie. Let’s do a pie analogy:
- We have a whole pie.
- We want everyone at the dinner to get the same amount of pie with no leftovers
- We know we are going to have either 2 or 3 people at the dinner.
- How can we divide up the pie so that regardless of whether 2 or 3 people show up, we can divide the pie evenly?
The question then becomes, what number of slices divides into both 2 and 3 without remainder? The answer lies in something you learned in elementary school, but probably didn’t care to remember how to calculate it: the Least (Lowest) Common Multiple (LCM). But wait, there’s more! In order to calculate the LCM, you need to know the Greatest Common Divisor (GCD) of the two numbers. Yay! Math! Fun!
Keep in mind, this proof is very non-rigorous, and probably has many holes and unwritten assumptions. But I hope it’ll make it logical how to find the LCM.
Numbers
A couple of terminology clarifications.
I’ll be saying “number” a lot, but what we really care about are only the natural (or counting) numbers: ![]() . So, you can replace any “number” with “natural number” or “positive integer“.
. So, you can replace any “number” with “natural number” or “positive integer“.
In this set of numbers, we call one number divisible by another if the remainder is exactly 0. You might say, “3 IS divisible by 2; you get 1.5!” Again, we are dealing with the set of natural numbers, and 1.5 is not in this set, so 3 is not divisible by 2.
A factor or divisor of a number divides that number, i.e. 2 is a factor 6, but 5 is not a factor of 6.
A Common Multiple
Most of you might recall that to find the LCM of two numbers, you should just multiply the two numbers together… or something. But let’s reason this out:
- A number
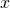 is always at least divisible by 1 and itself; there can be other factors, but the number itself and 1 must always be factors. (Think prime numbers: they are the least divisible numbers, besides 1, and even they are divisible by one and themselves.)
is always at least divisible by 1 and itself; there can be other factors, but the number itself and 1 must always be factors. (Think prime numbers: they are the least divisible numbers, besides 1, and even they are divisible by one and themselves.) - The easiest way to make any number into a multiple of another number
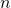 is to multiply by
is to multiply by 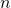 .
.
Fine, so we have a number ![]() , and its factors include at least 1 and
, and its factors include at least 1 and ![]() . If we want to make that number also a multiple of
. If we want to make that number also a multiple of ![]() , then we multiply the two together. Algebraically, the fact that this makes the resulting number a common multiple (ACM — my abbreviation) is obvious. (Note for people who don’t know algebra, when we write two variables right next to each other, we mean that they should be multiplied):
, then we multiply the two together. Algebraically, the fact that this makes the resulting number a common multiple (ACM — my abbreviation) is obvious. (Note for people who don’t know algebra, when we write two variables right next to each other, we mean that they should be multiplied):
![]()
You can divide ![]() by
by ![]() and get
and get ![]() and vice versa. And we can be sure that there is no remainder, because by definition,
and vice versa. And we can be sure that there is no remainder, because by definition, ![]() and
and ![]() are whole numbers.
are whole numbers.
Let’s call this ![]() product officially the ACM.
product officially the ACM.
The Least Common Multiple?
How can we be sure it’s the least common multiple? And if it isn’t, how can we make it the least?
Let’s assume for now that this ACM ![]() is not the LCM, and that there is a whole number
is not the LCM, and that there is a whole number ![]() that you can divide the ACM by to get the LCM. That means:
that you can divide the ACM by to get the LCM. That means:
![]()
Fine! So if this new fraction is indeed the LCM, we can then still divide by each of the original numbers (and get 0 remainder). Let’s see what we get if we do that:
![]()
So, since the remainder must be zero, that means that ![]() are both whole numbers, and thus
are both whole numbers, and thus ![]() must be a divisor/factor of both
must be a divisor/factor of both ![]() and
and ![]() . We now divide the ACM by
. We now divide the ACM by ![]() to get a new common multiple. If this new common multiple is not the least, then we should be able to find another common divisor of
to get a new common multiple. If this new common multiple is not the least, then we should be able to find another common divisor of ![]() and
and ![]() . Rinse and repeat until there are no more common divisors, in which case, we have found THE least common multiple.
. Rinse and repeat until there are no more common divisors, in which case, we have found THE least common multiple.
So all we have to do to go from ACM-> LCM is to continually divide by common divisors until there are no more common divisors besides 1 (since dividing by 1 doesn’t change anything).
Example:
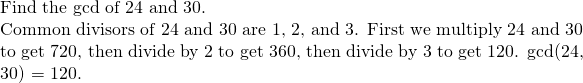
An easier way than dividing sequentially through all common divisors is just to find the greatest common divisor, and divide our ACM by it. Almost there.
Greatest Common Divisor
The GCD of two numbers is the largest whole number that divides both numbers without remainder. For example, ![]() and
and ![]() . You can check for yourself using these examples that the gcd is the largest number that will divide evenly both numbers. Sidenote: numbers that have a GCD of 1 are called coprime numbers.
. You can check for yourself using these examples that the gcd is the largest number that will divide evenly both numbers. Sidenote: numbers that have a GCD of 1 are called coprime numbers.
There are many methods for finding GCD, including the Euclidean Algorithm. For our purposes (since polyrhythms don’t tend to get that high in number), we can just try every number from smaller of the two numbers (whose GCD we are calculating) down to 1. If you get to one and haven’t found a number that divides into both, then the GCD is 1, and the numbers are coprime, in which case the ACM we calculated is equal to the LCM. Otherwise, you divide the ACM by the GCD to get the LCM.
The Least Common Multiple!
Let’s summarize the equation for finding the least common multiple:
![]()
So what do we do with this?
Method 1
Again, let’s do any easy example: 3:2 polyrhythm. First, we write down all the numbers:
![]()
Then, on the bottom, we want to ask ourselves, if two people showed up to our pie party, how many slices would each one get? ![]() . So on the bottom row, let’s write two groups of “123”
. So on the bottom row, let’s write two groups of “123”
![]()
Now, let’s put an X on the first of each group, and erase the rest:
Then you
![]()
The X’s are where the notes are going to be played. Do the same sort of thing for the top, except now it’s three groups of two (the pie divided among three people):
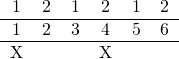
And then change the first of each groupinto X’s
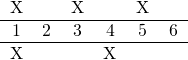
To read this chart, we count to 6, and on one hand we tap the top line, and the other the bottom. Now you have one way of thinking about 3:2 accurately – subdivide the beat into 6, and play the notes on their respective microbeats.
But, when the polyrhythms get more complex, it can result in a high LCM, and we don’t want to have to count to that high of a number. There’s a cyclical way to think about this chart, and we will do it with the same polyrhythm.
Method 2
For this method, you will choose one of the divisions to be the main “pulse.” In this case, since the duple is on the bottom, that will be the main pulse. We’re going start by doing the same thing as the previous method:
![]()
Now copy the bottom line to the middle line, and then put X’s on the bottom line first micro-beats, like so:
![]()
Next, let’s put our 3 groups of two on the top line:
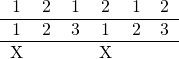
And then turn them into X’s:
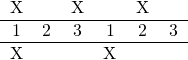
Last step, for each top X, copy the number directly under it and overwrite the X:
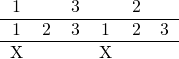
Though in writing this seems like a lot of steps, in practicality, you don’t need a lot of the intermediate steps once you know what’s going on.
To perform this, you tap or clap the bottom line, then you start saying the middle line quietly (or thinking it), and then once you get a good groove, you start accenting the numbers that fall on the top line. In graphical form, you would be doing something like this: 1 2 3 1 2 3, where the gray numbers you don’t say out loud, the magenta ones you do, and you clap on “1”.
This way of thinking about polyrhythms is how some conservatories teach you. Again, that is to clap the bottom line, think the middle line, and say the top line:
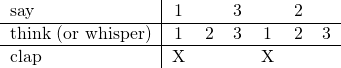
This table also gives you a visual aid to use if you want to tap, say, the right hand for the top line and left hand for the bottom line. You can see how things are supposed to line up.
Here’s one for 7:3 ( ![]() ) in both table versions:
) in both table versions:
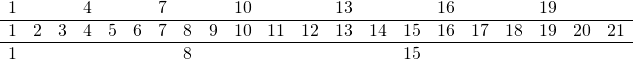
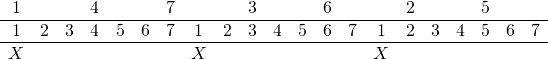
The second one is easier to count, right? (I mean, neither are particularly easy.)
Conclusion
Again, I want to make sure to emphasize that one should not be robotic about their performance of polyrhythms. However, knowing how it should mathematically work allows you to know what the baseline is. And with modern music, sometimes you have to do it precisely! I hope this and the tool on the labs will help you. Again, check out labs.seanchenpiano.com/polyrhythms! The default (non-verbose) mode on the metronome shows you the cyclical way of counting (method 2), and the verbose mode shows you everything!

